Operator Overloading In Python

Python is a versatile and powerful programming language that offers various features to make code more expressive and concise. One such feature is operator overloading, which allows developers to redefine the behavior of operators such as +, -, *, /, and more.

By implementing operator overloading, we can extend the capabilities of built-in operators to work with custom objects and classes. This article dives into the concept of operator overloading in Python, exploring its benefits and demonstrating how it can be effectively used.

Operator Overloading 101

What is it?

Operator overloading refers to the ability to redefine the behavior of an operator for custom objects, i.e. it enables the seamless interaction of user-defined objects with infix operators such as + and |, as well as unary operators like - and ~.

Although it is criticized in certain communities, it is a language feature that, when misused, can result in programmer confusion, bugs, and unforeseen performance issues. However, when used properly, it leads to easily understandable code and APIs. Python achieves a favorable balance between flexibility, usability, and safety by imposing certain restrictions:

1. The meaning of operators for built-in types cannot be altered.
2. Only existing operators can be overloaded, i.e. we cannot create new operators.
3. Some operators, such as is, and, or, and not, cannot be overloaded, although bitwise operators like &, |, and ~ can be overloaded.

Benefits of operator overloading

We can notice different pros such as:

1. Enhanced Readability: By overloading operators, we can make our code more readable and expressive. It enables us to use familiar syntax with custom objects, making our code resemble the operations performed on built-in types.
2. Customized Behaviors: Operator overloading allows us to define specific behaviors for operators based on the context of our classes. For example, we can define addition (+) to concatenate strings or merge data structures, or define multiplication (*) to repeat elements in a custom sequence.
3. Code Reusability: By implementing operator overloading, we can reuse existing operators for our custom classes, reducing the need to write separate methods for each operation. This promotes code reusability and saves development time.

Overloading Unary Operators

Unary operators in Python are operators that perform operations on a single operand. They allow us to manipulate the value of a single object or variable. Python provides several unary operators, including:

• Unary Minus Operator (-), implemented by __neg__:
  This operator represents arithmetic unary negation. For example, if the value of x is -2, then the expression -x evaluates to 2.
• Unary Plus Operator (+), implemented by __pos__:
  This operator represents arithmetic unary plus. In most cases, x is equal to +x. However, there are a few scenarios where this equality does not hold true. .
• Bitwise Complement Operator (~), implemented by __invert__:
  This operator performs bitwise negation or bitwise inverse on an integer. It is defined as ~x == -(x+1). For instance, if the value of x is 2, then ~x evaluates to -3.

class Vector:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def __neg__(self):
        return Vector(-self.x, -self.y)

    def __pos__(self):
        return Vector(+self.x, +self.y)
        
    def __invert__(self):
        return Vector(~self.x, ~self.y)

These special methods associated with the unary operators enable customized behavior and functionality when working with objects or variables in Python.

Overloading Arithmetic Operators

To illustrate the addition and multiplication operator overloading, we will pick up an old example of the Vector Class.

Although the official Python documentation states that sequences should use the + operator for concatenation and * for repetition, in the case of the Vector class, we will redefine the behavior of + and * to represent mathematical vector operations.

Addition Operator and Mixed Type Addition

Starting with the + operator, we overload it as such:

from array import array
import reprlib
import math
import itertools    


class Vector:
    typecode = "d"
    __match_args__ = ("x", "y", "z", "t")

    def __init__(self, components):
        self._components = array(self.typecode, components)

    def __iter__(self):
        return iter(self._components)

    def __repr__(self):
        components = reprlib.repr(self._components)
        components = components[components.find("[") : -1]
        return f"Vector({components})"

    def __str__(self):
        return str(tuple(self))

    def __bytes__(self):
        return bytes([ord(self.typecode)]) + bytes(self._components)

    def __abs__(self):
        return math.hypot(*self)

    def __bool__(self):
        return bool(abs(self))

    def __len__(self):
        return len(self._components)

    def __getitem__(self, key):
        if isinstance(key, slice):
            cls = type(self)
            return cls(self._components[key])
        index = operator.index(key)
        return self._components[index]

    def __eq__(self, other):
        if len(self) != len(other):
            return False
        for a, b in zip(self, other):
            if a != b:
                return False
        return True

    def __hash__(self):
        hashes = (hash(x) for x in self._components)
        return functools.reduce(operator.xor, hashes, 0)

    def __add__(self, other):
        pairs = itertools.zip_longest(self, other, fillvalue=0.0)
        return Vector(a + b for a, b in pairs)
        
    def __radd__(self, other):
        return self + other
        
v1 = Vector([3, 4, 5, 6])
v3 = Vector([1, 2])
print(v1 + v3)
# (4.0, 6.0, 5.0, 6.0)
print((10, 20, 30) + v1)
# (13.0, 24.0, 35.0, 6.0)

In order to facilitate operations involving objects of different types, Python incorporates a specialized dispatching mechanism for the infix operator special methods. When encountering an expression such as a + b, the interpreter follows a series of steps:

• If object a possesses the __add__ method, the interpreter invokes        a.__add__ (b) and returns the result, unless the method returns NotImplemented.
• If object a lacks the __add__ method or its invocation returns NotImplemented, the interpreter checks whether object b has the __radd__ method (reverse add). If present, it calls b.__radd__ (a) and returns the result, unless the method returns NotImplemented.
• If object b does not have the __radd__ method or its invocation returns NotImplemented, the interpreter raises a TypeError with a message indicating unsupported operand types.

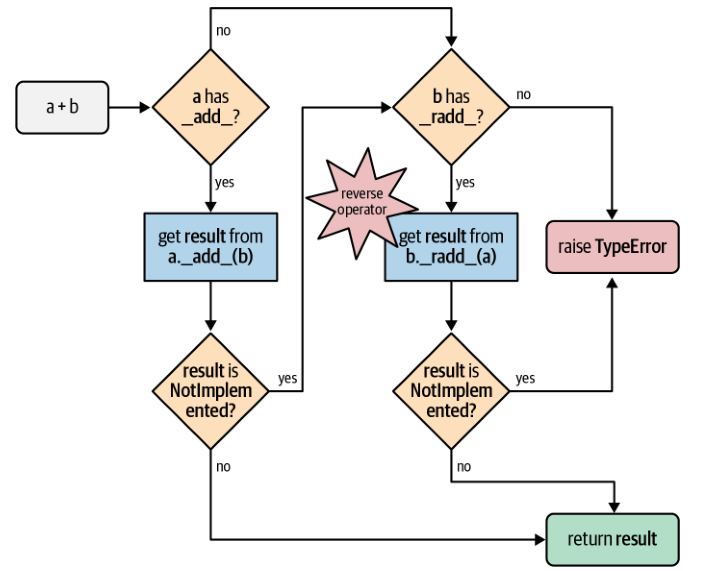
This mechanism ensures that Python gracefully handles operations involving objects of diverse types, attempting various avenues for finding a suitable method implementation.

Multiplication Operator and Mixed Type Multiplication

To enable mixed type multiplication and support scalar multiplication, we will implement the __mul__ method for regular multiplication and the __rmul__ method for reverse multiplication.

from array import array
import reprlib
import math
import itertools    


class Vector:
    typecode = "d"
    __match_args__ = ("x", "y", "z", "t")

    def __init__(self, components):
        self._components = array(self.typecode, components)

    # many methods omitted, check previous examples
    # many methods omitted, check previous examples
    # many methods omitted, check previous examples
    
    def __add__(self, other):
        pairs = itertools.zip_longest(self, other, fillvalue=0.0)
        return Vector(a + b for a, b in pairs)
        
    def __radd__(self, other):
        return self + other
        
    def __mul__(self, scalar):
        try:
            factor = float(scalar)
        except TypeError:
            return NotImplemented
        return Vector(n * factor for n in self)

    def __rmul__(self, scalar):
        return self * scalar
        
v1 = Vector([3, 4, 5, 6])
print(14*v1)
# (42.0, 56.0, 70.0, 84.0)

To facilitate Vector by Vector multiplication, we will use a distinct infix operator, specifically the "@" symbol, to denote this operation.

The special methods __matmul__, __rmatmul__, and __imatmul__ are associated with the "@" operator, which is named after matrix multiplication. Although these methods are currently not used within the standard library, they are recognized by the Python interpreter starting from Python 3. They provide support for the "@" operator and enable custom matrix multiplication operations.

from array import array
import reprlib
import math
import itertools    
from collections.abc import Sized, Iterable


class Vector:
    typecode = "d"
    __match_args__ = ("x", "y", "z", "t")

    def __init__(self, components):
        self._components = array(self.typecode, components)

    # many methods omitted, check previous examples
    # many methods omitted, check previous examples
    # many methods omitted, check previous examples

    def __add__(self, other):
        pairs = itertools.zip_longest(self, other, fillvalue=0.0)
        return Vector(a + b for a, b in pairs)
        
    def __radd__(self, other):
        return self + other
        
    def __mul__(self, scalar):
        try:
            factor = float(scalar)
        except TypeError:
            return NotImplemented
        return Vector(n * factor for n in self)

    def __rmul__(self, scalar):
        return self * scalar
        
    def __matmul__(self, other):
        if (isinstance(other, Sized) and isinstance(other, Iterable)):
            if len(self) == len(other):
                return sum(a * b for a, b in zip(self, other))
            else:
                raise ValueError('@ requires vectors of equal length.')
        else:
            return NotImplemented

    def __rmatmul__(self, other):
        return self @ other

va = Vector([1, 2, 3])
vz = Vector([5, 6, 7])
print(va @ vz) 
# 38.0
print ([10, 20, 30] @ vz)
# 380.0

Overview of Arithmetic Operators

By implementing the addition (+), multiplication (*), and matrix multiplication (@) operations, we have explored the fundamental patterns for coding infix operators. The techniques we have discussed can be applied to all the operators listed below, allowing for consistent and customizable behavior across a wide range of operations.

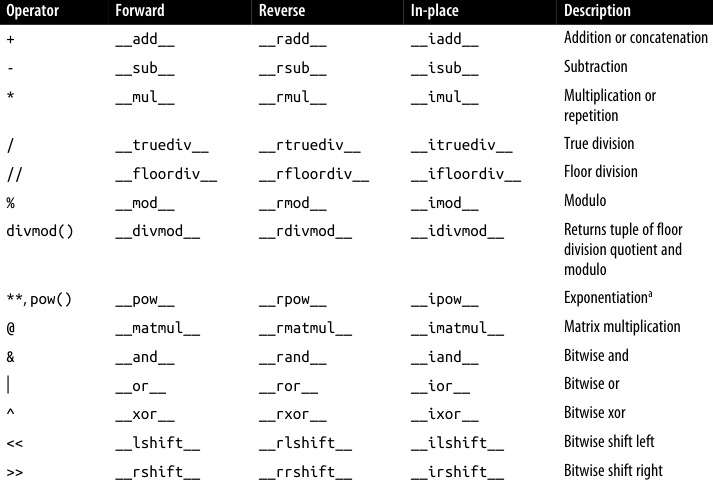
Overloading Comparison Operators

The Python interpreter handles the comparison operators (==, !=, >, <, >=, and <=) in a manner similar to what we have discussed earlier, but with two significant differences:

• Use of the same set of methods in forward and reverse operator calls, for example a forward call to __gt__ (greater than) is followed by a reverse call to __lt__ (less than), but with the arguments reversed.
• Handling of == and != when the reverse method is missing is different, Python resorts to comparing the object IDs instead of raising a TypeError. This behavior allows for comparison of objects that do not explicitly define the reverse method.

These differences in handling the comparison operators provide flexibility and fallback options in case the reverse method is not implemented. It ensures that the comparison operations can still be performed effectively by resorting to alternate comparison strategies, such as comparing object IDs.

from array import array
import reprlib
import math
import itertools    
from collections.abc import Sized, Iterable


class Vector:
    typecode = "d"
    __match_args__ = ("x", "y", "z", "t")

    def __init__(self, components):
        self._components = array(self.typecode, components)

    # many methods omitted, check previous examples
    # many methods omitted, check previous examples
    # many methods omitted, check previous examples
        
    def __eq__(self, other):
        if isinstance(other, Vector):
            return (len(self) == len(other) and all(a == b for a, b in zip(self, other)))
        else:
            return NotImplemented

va = Vector([1.0, 2.0, 3.0])
vb = Vector(range(1, 4))
print(va == vb)
# True

Overloading Augmented Assignment Operators

To implement augmented assignment operators in Python, we need to define the special methods that correspond to the desired operators. For example:

• Addition and Assignment (+=): __iadd__(self, other)
  This method is called when the += operator is used. It should modify the current object's state by adding the value of other and return the modified object.
• Subtraction and Assignment (-=): __isub__(self, other)
  This method is called when the -= operator is used. It should modify the current object's state by subtracting the value of other and return the modified object.
• Multiplication and Assignment (*=): __imul__(self, other)
  This method is called when the *= operator is used. It should modify the current object's state by multiplying it with the value of other and return the modified object.
• Division and Assignment (/=): __idiv__(self, other)
  This method is called when the /= operator is used. It should modify the current object's state by dividing it by the value of other and return the modified object.
• Modulo and Assignment (%=): __imod__(self, other)
  This method is called when the %= operator is used. It should modify the current object's state by applying the modulo operation with the value of other and return the modified object.
• Bitwise AND and Assignment: __iand__(self, other)
• Bitwise OR and Assignment: __ior__(self, other)
• Bitwise XOR and Assignment: __ixor__(self, other)

These methods should be implemented in our class to define the behavior of augmented assignment operators when applied to instances of that class. They should modify the object's state accordingly and return the modified object.

class TestClass:

    def __init__(self, value):
        self.value = value

    def __iadd__(self, other):
        self.value += other
        return self

    def __isub__(self, other):
        self.value -= other
        return self

    def __imul__(self, other):
        self.value *= other
        return self

    def __idiv__(self, other):
        self.value /= other
        return self

    def __imod__(self, other):
        self.value %= other
        return self

    def __iand__(self, other):
        self.value &= other
        return self

    def __ior__(self, other):
        self.value |= other
        return self

    def __ixor__(self, other):
        self.value ^= other
        return self

Conclusion

Operator overloading is a powerful feature in Python that allows us to redefine the behavior of operators for custom classes. It provides enhanced readability, customized behaviors, and code reusability. By leveraging operator overloading effectively, we can create more expressive and intuitive code, improving the overall design and functionality of our Python programs.

Further Reading

• The "Why operators are useful" article.
• the “Data Model” chapter of the Python documentation.